Documentation - Example 2

DOCUMENTATION FOR MATHS::SPECIAL::BESSELL::I::BESSEL I

This example shows more uses of Doxygen, including more equations and how to insert a graph:

Brief Description


Modified Bessel function of the first kind of integer order.
Gives this (one part is grayed out due to there being two functions within this module):

Interface
#include <codecogs/maths/special/bessel/i.h>
double  Maths::Special::Bessel::besselI(double x, double v)
  Modified Bessel function of the first kind.
double  Maths::Special::Bessel::besselI (double x, int v)
  Modified Bessel function of the first kind of integer order.

Detailed Description

These function return solutions to the Modified Bessel Function of the first kind.

The differential equation
\[   z^2 \frac{d^2y}{dz^2} + z \frac{dy}{dz} - (z^2 + v^2)y = 0 \]
where \e v is a real constant, is called the modified Bessel's equation, with the solution known as the modified Bessel function,
with two fundamental solutions: $ I_v(z)$ and $I_{-v}(z)$, where 

\[ I_{v}(z) = \frac{z}{2}^v \sum_{k=0}^{\infty} \frac{\left ( \frac{z^2}{4}^k \right )}{k! \Gamma(v+k+1)} \]

where $\Gamma(n)$ is the gamma function.

\image html besselI.gif "The Bessel function at varying orders"

A second solution, which is independent of $ I_{v}(z)$, is known as the modified Bessel function of the second kind \ref besselK. 
\References
http://mathworld.wolfram.com/ModifiedBesselFunctionoftheFirstKind.html
Gives this:

Detailed Description

These function return solutions to the Modified Bessel Function of the first kind.

The differential equation

\[ z^2 \frac{d^2y}{dz^2} + z \frac{dy}{dz} - (z^2 + v^2)y = 0 \]

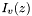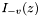where v is a real constant, is called the modified Bessel's equation, with the solution known as the modified Bessel function, with two fundamental solutions: $ I_v(z)$ and $I_{-v}(z)$, where

\[ I_{v}(z) = \frac{z}{2}^v \sum_{k=0}^{\infty} \frac{\left ( \frac{z^2}{4}^k \right )}{k! \Gamma(v+k+1)} \]

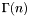where $\Gamma(n)$ is the gamma function.
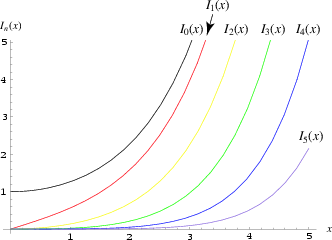
besselI.gif

The Bessel function at varying orders

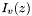A second solution, which is independent of $ I_{v}(z)$, is known as the modified Bessel function of the second kind besselK.
Reference
http://mathworld.wolfram.com/ModifiedBesselFunctionoftheFirstKind.html

The Source Code (+ Function Description)

//! Modified Bessel function of the first kind.
/*!  
Returns modified Bessel function of the first kinds for any order (\a v)

The function is defined as \f$ I_1(x) = -i J_1(ix)\f$

The range is partitioned into the two intervals [0,8] and (8, infinity). Chebyshev polynomial expansions are employed in each interval.

\param x input argument.
\param v order of bessel function.

\par Accuracy:

Relative error:
arithmetic   domain     # trials      peak         rms
DEC       0, 30        3400       1.2e-16     2.3e-17
IEEE      0, 30       30000       1.9e-15     2.1e-16

\Example
\code
#include 
#include 

int main()
{
  using namespace Maths::Special::Bessel;
  printf("\n  x      v=0      v=1      v=2      v=3      v=4      v=5");
  for(double x=0; x<6; x++)
  {
    printf("\nx=%.1lf",x);
    for(int v=0;v<=5;v++)
      printf(" %8.6lf", besselI(x,v));
  }  
  return 0;
}
\endcode

\Output
\code
x      v=0      v=1      v=2      v=3      v=4      v=5
x=0.0 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000
x=1.0 1.266066 0.565159 0.135748 0.022168 0.002737 0.000271
x=2.0 2.279585 1.590637 0.688948 0.212740 0.050729 0.009826
x=3.0 4.880793 3.953370 2.245212 0.959754 0.325705 0.091206
x=4.0 11.301922 9.759465 6.422189 3.337276 1.416276 0.504724
x=5.0 27.239872 24.335642 17.505615 10.331150 5.108235 2.157975
\endcode
\author Stephen L. Moshier. Copyright 1984, 1987, 2000  
\author Documentation by Will Bateman
\References
Cephes Math Library Release 2.8:  June, 2000
*/
double besselI(double x, double v)
{
  ...
}
Gives this:
double besselI (  double  x,
double  v
) 
Returns modified Bessel function of the first kinds for any order (v)

The function is defined as 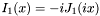$ I_1(x) = -i J_1(ix)$

The range is partitioned into the two intervals [0,8] and (8, infinity). Chebyshev polynomial expansions are employed in each interval.

Parameters:
x  input argument.
v  order of bessel function.
Accuracy:
Relative error:
arithmetic   domain     # trials      peak         rms
DEC       0, 30        3400       1.2e-16     2.3e-17
IEEE      0, 30       30000       1.9e-15     2.1e-16
Example:
#include <codecogs/maths/special/bessel/i.h>
#include <stdio.h>

int main()
{
  using namespace Maths::Special::Bessel;
  printf("\n  x      v=0      v=1      v=2      v=3      v=4      v=5");
  for(double x=0; x<6; x++)
  {
    printf("\nx=%.1lf",x);
    for(int v=0;v<=5;v++)
      printf(" %8.6lf", besselI(x,v));
  }  
  return 0;
}
Example Output:
x      v=0      v=1      v=2      v=3      v=4      v=5
x=0.0 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000
x=1.0 1.266066 0.565159 0.135748 0.022168 0.002737 0.000271
x=2.0 2.279585 1.590637 0.688948 0.212740 0.050729 0.009826
x=3.0 4.880793 3.953370 2.245212 0.959754 0.325705 0.091206
x=4.0 11.301922 9.759465 6.422189 3.337276 1.416276 0.504724
x=5.0 27.239872 24.335642 17.505615 10.331150 5.108235 2.157975
Author:
Stephen L. Moshier. Copyright 1984, 1987, 2000
Documentation by Will Bateman
References:
Cephes Math Library Release 2.8: June, 2000
Source Code:

You only own a GNU GPL licence for this module.
You do not own any licences for this module.

view or hide the source code

Other Example Pages