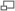Engineering › Fluid Mechanics › Machines › Turbines ›

Water Turbines

This section covers the analysis of water turbines and the selection of turbines for a particular application

View other versions (6)

Contents

Water Turbines
Stationary Curved Vanes
A Series Of Moving Curved Vanes.
Turbine With Curved Vanes And An Inward Radial Flow (francis Or Gerard Turbine)
Efficiency Of Turbines
Impulse Turbine Allowing For Friction
Reaction Turbines
Characteristic Curves And Iso-efficiency Curves For A Turbine Under All Operating Conditions
Page Comments

Water Turbines

Hydro electricity is a reliable form of renewable energy. Water turbines are highly efficient and easily controlled to provide power as and when it is needed. In addition, the only system currently available to store large quantities of electrical power is pumped storage.

General Approach To Find Force, Work Done, Efficiency, Etc.

Find the mass of liquid/sec. striking the vanes ( slugs/sec or kilograms/sec).
Find the change in absolute (or relative) velocity of the liquid in the required direction. (ft/sec. or meters/sec.)
Force on the vane in this direction (Newton's second Law) equals mass/sec $\inline X$ change of velocity. ( slugs/sec $\inline X$ ft/sec = lb. or kg/sec $\inline X$ mtr./sec = Newtons)
The vane exerts an equal and opposite reaction on the liquid and the supply nozzle. (Jet reaction)
Work done / sec. by the liquid on the vane is the vane velocity $\inline X$ force on plate in the direction of the velocity. (ft.lb./sec. or Watts)
Horse Power output = Work done per sec. $\inline \div 550$
Efficiency, $\inline \eta$ = Output Power/ Input power from jet

Series Of Moving Plates

A turbine is a rotary engine that extracts energy from a fluid flow and converts it into useful work.

A water turbine is a rotary engine that takes energy from moving water.

Assume that the water leaves the plates tangentially:

MISSING IMAGE!

23287/Intro-to-Turbines-001.png cannot be found in /users/23287/Intro-to-Turbines-001.png. Please contact the submission author.

The weight of water hitting the plates per second $\inline = W = waV$ . N.B. For a single plate the weight of water per second striking the plate is $\inline wa(V-v)$
The change of velocity = $\inline (V - v)$
Force on plate = mass/sec. $\inline X$ Change of velocity $\inline = \displaystyle\frac{W}{g}\left(V - v \right)$
Work done/second = Force $\inline X$ Velocity $\inline = \displaystyle\frac{W}{g}\left(V - v \right)v$
The input = the Kinetic energy of the jet $\inline = \displaystyle\frac{WV^2}{2g}$
The efficiency of the system, $\inline \eta = \displaystyle\frac{2\,v(V - v)}{V^2}$
For a given jet velocity, $\inline \displaystyle\frac{d\eta }{dv} = \displaystyle\frac{2}{V^2}\left(V - v \right)$
For maximum $\inline \eta$ , $\inline V = 2v$ and the value of the maximum efficiency $\inline \eta = 50\%$ .

A Single Plate Inclined To The Jet.

The normal force is the component, perpendicular to the surface of contact, of the contact force exerted on an object by, for example, the surface of a floor or wall, preventing the object from penetrating the surface.

Neglecting friction and assuming that the water leaves the plate tangentially, the resulting force will be normal to the plate.

MISSING IMAGE!

23287/Intro-to-Turbines-002.png cannot be found in /users/23287/Intro-to-Turbines-002.png. Please contact the submission author.

The weight of water striking the plate per second will be, as before, given by:
$W = w\,a(V - v)$
Change of velocity normal to the plate = $\inline (V - v)\,sin\,\theta$
Normal force on plate $\inline F = \displaystyle\frac{w\,a\,(v - v)\;sin\,\theta }{g}$
Component of $\inline F$ in the direction of $\inline v = F\;sin\,\theta = \displaystyle\frac{wa\;(v - v)^2\;sin^2\theta}{g}$
Work done on plate $\inline = sin\,\theta \times v\ = \displaystyle\frac{w\,a\,(V - v)^2\;vsin^2\theta }{g}$

Stationary Curved Vanes

MISSING IMAGE!

23287/Intro-to-Turbines-003.png cannot be found in /users/23287/Intro-to-Turbines-003.png. Please contact the submission author.

Force in the direction of $\inline x = \displaystyle\frac{W}{g}(V \cos\,\alpha - V_1 \cos\,\beta )\ = \frac{W}{g}(V_w - V_{w1})$ N.B. $\inline \;W_{w1}$ is negative.

For a semi circular blade both $\inline \alpha$ and $\inline \beta$ are zero and neglecting friction the force is twice that of a corresponding flat plate.

Force in direction $\inline y = \displaystyle\frac{W}{g}(V_f - V_{f1})$

A Series Of Moving Curved Vanes.

Relative velocity is the vector difference between the velocities of two objects, as evaluated in terms of a single coordinate system.

Absolute velocity is the vector sum of the velocity of a fluid parcel relative to the earth and the velocity of the parcel due to the earth's rotation

The following symbols are used in the construction of velocity triangles.

$\inline V_r =$ Relative velocity and is tangential to the blades.
$\inline v =$ Blade velocity (Add to $\inline V_r$ )
$\inline V =$ Absolute velocity and the vector sum of $\inline v$ and $\inline V_r$ .

(The arrows of $\inline v$ and $\inline v_r$ must follow each other round the triangle.)

$\inline V_w =$ The velocity of whirl (Component of $\inline V$ in the direction of $\inline v$ )
$\inline V_f =$ The velocity of flow (Component of $\inline V$ normal to direction of $\inline v$ )

The suffix 1 refers to the outlet triangle.

$\inline \alpha \;and\;\beta$ are the inlet and outlet angles of absolute velocity (i.e.Jet 0)

$\inline \theta$ and $\inline \phi$ are the inlet and outlet angles relative to the blade velocity.

Axial Flow Turbine

The inlet and outlet triangles at different speeds:

Low Speed

MISSING IMAGE!

23287/IR-Turbines-004.png cannot be found in /users/23287/IR-Turbines-004.png. Please contact the submission author.

High Speed

The outlet triangle remains the same but the inlet triangle is now:

MISSING IMAGE!

23287/IR-Turbines-007.png cannot be found in /users/23287/IR-Turbines-007.png. Please contact the submission author.

Note: $\inline v = v_1$ and $\inline V_r = V_{r1}$ if there is no friction

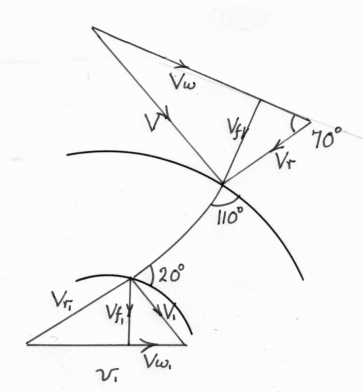
Pelton Wheel (circumferential)

The two velocity triangles are for low and high flow (the inlet triangle is a straight line):

MISSING IMAGE!

23287/IR-Turbines-pl.png cannot be found in /users/23287/IR-Turbines-pl.png. Please contact the submission author.

For both types of flow above:

Jet velocity $\inline = C_v\;\sqrt{2gH}$ , where $\inline H$ is the head behind the nozzle and $\inline C_v$ is the Velocity coefficient.
Weight of water per second $\inline W = w\;a\;V$
The blade speed, $\inline v = \displaystyle\frac{\pi \,d\,N}{60}$
Force on the vanes = mass of water/second, $\inline X$
Change in velocity $\inline = \displaystyle\frac{W}{g}\left(V_w - V_{w1} \right)$
Work done on the vanes = Force $\inline X$ Velocity $\inline = \displaystyle\frac{W}{g}\left(V_w - V_{w1} \right)$
The Kinetic energy supplied $\inline = \displaystyle\frac{W\,V^2}{2g}$
The efficiency, $\inline \eta$ = Work done / K.E. supplied

Therefore

$\eta = \frac{2\,v(V_1 - V_{w1})}{V^2}$

For a Pelton Wheel Only

$V_w = V$ , $V_{r1} = V_r$

(if friction is ignored)

$\therefore \;\;\;\;\;V_{r1} = V - v$

But

$V_{w1} + v_1 = V_{r1}\,cos\phi\ = (V - v)\;cos\phi$

$\therefore\;\;\;\;\;V_{w1} = (V - v)\;cos\phi - v$

$\eta = \displaystyle\frac{2v}{V^2}\left(V_w - V_{w1}\right)}\= \frac{2v}{V^2}\left[(V - v) + (V - v)cos\phi \right]$

(2)

For the maximum $\inline \eta$ at a given head and blade angle: $\inline \displaystyle\frac{d\eta }{dv} = 0$

Which occurs when

$v = \displaystyle\frac{V}{2}$

i.e. The bucket speed is half the jet speed. This is a theoretical figure and in practice, due to frictional losses, the maximum efficiency is when $\inline v\;\approx \;0.47\;V$

Example:

[imperial]

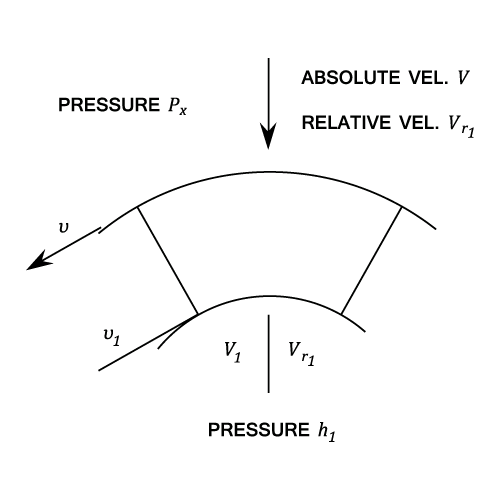
Example - Example 1

Problem

The diagram shows a section of a Pelton wheel which has a 2 in. Diam. Jet which produces 2 cubic ft. of water per second. The blade speed is 40 ft/sec and due to friction $\;V_{r1} = 0.9\;V_r$ . ( 1 cubic foot of water weighs 62.4 lbs. and $g$ = 32.2 ft/s)

Workings

To find the force in the $X$ direction.

Jet $V$ $= \displaystyle\frac{Q}{area} = \displaystyle\frac{2}{\displaystyle\frac{\pi }{4}\times \displaystyle\frac{1}{36}} = 91.7 ft/sec.$ . Therefore, $V_w\;=91.7\,ft/sec$

$v_r = V - v = 91.7 - 40 = 51.7ft/sec$

And $V_{r1} = 0.9V_r = 46.53ft/sec.$

From the outlet triangle:

$(v_1 - V_{w1}) = V_{r1}\times cos45^0 = \frac{46.53}{\sqrt{3}} = 32.9ft/sec.$

And $V_{r1} = 40 - 32.9 = 7.1ft/sec.$

Also $V_{f1} = 32.9ft/sec$

In the $X$ direction the Force on the vanes = mass of water $X$ change of velocity

$= \frac{2\times 62.4}{32.2}\times \left(91.7 - 7.1 \right) = 328 lbs.$

Force on vanes in the $Y$ direction =

$\frac{2\times 62.4}{32.2}\left(0 - 32.9 \right) = 127.5lbs.$

Therefore, the resultant force $= \sqrt{328^2 + 127.5^2} = 352lbs.$

The resultant is at $tan^{-1}\;\displaystyle\frac{127.5}{328}$ i.e. at $21^0\;14'$ to the direction of motion.

Work done per second on the vanes = The force in the $X$ direction times blade velocity

$= 328\times 40 = 13,120\;ft\,lbs/sec$

The Kinetic energy supplied by the jet per second

$= \frac{W\,V^2}{2g} = \frac{2\times 62.4\times 91.7^2}{2\times 32.2} = 16,280\;ft\,lbs/sec.$

Thus the efficiency of the turbine $= \displaystyle\frac{13220}{16280} = 80.6\%$

Solution

The efficiency of the turbine is $80.6\%$

Turbine With Curved Vanes And An Inward Radial Flow (francis Or Gerard Turbine)

The following diagram shows the velocity triangles for both low and high speed.

MISSING IMAGE!

23287/IR-Turbines-radial.png cannot be found in /users/23287/IR-Turbines-radial.png. Please contact the submission author.

Let the weight of water/second striking the vanes be $\inline W$ lb/sec.
Tangential momentum/second at entry $\inline = \displaystyle\frac{W}{g}V_w$
Moment of momentum at entry $\inline = \displaystyle\frac{W}{g}V_w\times v$
Moment of momentum at outlet $\inline = \displaystyle\frac{W}{g}(V_{w_1}\times v_1)$
Torque on the vanes equals the change of moment of momentum per second

$=\frac{W}{g}\left(V_w\,v - V_{w1}\,v_1 \right)$

The work done per second on the vanes equals the Torque times the angular velocity

$= \frac{W}{g}\left(V_w\,v - V_{w1}\,v_1 \right)\Omega$

but

$\Omega r = v$ and $\Omega r_1 = v_1$

Therefore work done/second $\inline = \displaystyle\frac{W}{g}\left(V_w\,v -V_{w1}\,v_1\right)$

Euler Equation

$Power= $\displaystyle\frac{W}{g}\left(V_w\,v -V_{w1}\,v_1\right)$

which can be applied to any type of turbine or centrifugal pumps.

Efficiency Of Turbines

Impulse Turbines (No allowance for frictional losses)

MISSING IMAGE!

23287/Efficiency-of-Turbines-004.png cannot be found in /users/23287/Efficiency-of-Turbines-004.png. Please contact the submission author.

$\inline H$ is the total head behind the nozzle i.e. the sum of the pressure and velocity heads

$= H_1 - L \left(\frac{4flv^2}{2dg} \right)$

(where $\inline L$ represents the pipe line losses)
$\inline V =$ Jet Velocity

$\inline V_1$ = the exhaust velocity of water leaving the vanes.

$V = \sqrt{2gH} = \sqrt{2g(H_1 - L)}$

Work done per second on the vanes (per lb of water per second)

$= H - \frac{v_1^2}{2g} = \frac{V^2}{2g} - \frac{V_1^2}{2g} = \frac{V_w - V{_w1}}{g}$

The theoretical hydraulic efficiency of the Turbine is equal to:

$\frac{H - \displaystyle\frac{V_1^2}{2g}}{H} = \frac{V^2 - V_1^2}{V^2} = \frac{V_wv - V_{w1}v_1}{gH}$

Impulse Turbine Allowing For Friction

Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other.

The friction losses in the nozzle - $\inline h_n$ running and mechanical losses - $\inline h_m$

The effect of friction is to reduce $\inline V$ i.e. to reduce the hydraulic height $\inline \eta$

$V = C_v\sqrt{2gH}$

$h_n = H(1 - C_v^2) = \frac{v^2}{2g}\left(\frac{1}{C_v^2} - 1 \right)$

The Actual Hydraulic Efficiency of the Turbine

$= \frac{H-\displaystyle\frac{V_1^2}{2g} - h_n - h_m}{H}\ = \frac{V_wv - V_{w1}v_1}{gH}$

The latter is based upon value obtained from the velocity triangles and momentum considerations and will thus take into account the various changes in velocity due to friction.

The Actual (overall efficiency) is based on the useful work out divided by the water power input. It therefore makes allowance for the frictional losses.

MISSING IMAGE!

23287/Efficiency-of-Turbines-005.png cannot be found in /users/23287/Efficiency-of-Turbines-005.png. Please contact the submission author.

Example:

[imperial]

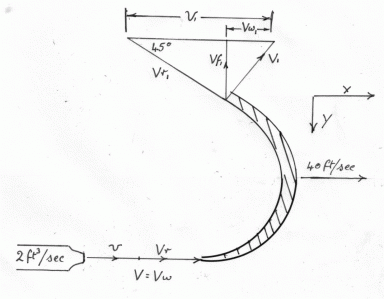
Example - Example 1

Problem

A Pelton wheel is driven by two similar jets, transmits 5000 Horse Power to the shaft running at 375 r.p.m. The head from the reservoir level is 670 ft. and the efficiency of power transmission through the pipeline and nozzles is 90%. The centre lines of the jets are tangential to a 4.8 ft. diameter circle. The relative velocity decreases by 10% as the water traverses the bucket surfaces which are so shaped that they would, if stationary deflect the water through an angle of 165 degrees.

( one Horse Power (HP) is 550 ft.lb/sec. One cubic ft. of water weighs 62.4 lb., $g =$ 32.2 ft/second squared)

Neglecting windage losses, find:

a) The efficiency of the runner.
b) The diameter of each jet.

Workings

Velocity head of jet = 0.9 $X$ gross head

$\frac{V^2}{2g} = 0.9\times 670$

$\therefore\;\;\;\;V = 197 ft/sec. = V_w$

$v = v_1 = \frac{\pi dN}{60} = \frac{\pi \times 4.8\times 375}{60} = 94.3\;ft/sec.$

$V_r = V - v\;=197 - 94.3 = 102.7 ft/sec.$

$V_{r1} = 0.9V_r = 92.5\;ft/sec.$

$v - V_{w1} = V_{r1}\;cos\,15^0 = 89.4\;ft/sec.$

$\therefore\;\;\;\;V_{w1} = 94.3 - 89.4 = 4.9 ft/sec = 93.3\%$

Hence the hydraulic efficiency of the runner:

$= \frac{V_wv - V_{w1}v_1}{g}\;\div \frac{V^2}{2g} = 93.3\%$

If there are no mechanical losses:

$W\left(\frac{V_wv - V_{w1}v_1}{g} \right)\div 550 = 5000$

Whence $W = 4890 lb/sec$ .

Quantity/Jet $= \displaystyle\frac{4890}{2\times 62.4} = 39.2 ft^3/sec.$

$\therefore\;\;\;\;\;\frac{\pi }{4}d_n^2\times 197 = 39.2$

Therefore the nozzle diameter is $0.503 ft$ . 0r approx. $6$ inches.

Solution

a) The efficiency of the runner is $93.3\%.$
b) The diameter of each jet is $0.503$ or approx. $6$ inches.

Reaction Turbines

Inward radial flow, mixed flow, or axial with a propeller shaft. They may be sited below the tail race or above it with a draft tube.

MISSING IMAGE!

23287/Efficiency-of-Turbines-002.png cannot be found in /users/23287/Efficiency-of-Turbines-002.png. Please contact the submission author.

$\inline V=$ The absolute velocity at the entry of the runner
$\inline v_1=$ The absolute velocity at the exit of the runner
$\inline h=$ the head.

Low Supply Head

Usually an open flume supply with a short Pinstock. e.g. Propeller Turbine. $\inline H$ is the vertical height from the water level in the forebay to the level in the Tail Race.

Large Head

Long Pinstock and smaller water through put e.g. Radial flow Francis Turbine. $\inline H$ is now the total head (i.e. Pressure, Velocity and Datum) in the supply pipe just before entering the Turbine casing and is relative to the tail stock Datum.

The Gross Head in this case is measured from the supply reservoir and includes Pinstock losses.

Draft Tube

This is designed to convert Kinetic Energy of discharge into Pressure. This gives extra suction through the Turbine. i.e. It enables the height $\inline Z$ ( see diag) to be included into the Supply head $\inline H$ .

Apply Bernoulli at $\inline A$ and $\inline C$ (see diag)

$\frac{p_a}{w} = \frac{v_a^2}{2g} + Z = \frac{p_b}{w} + \frac{v_b^2}{2g}$

(neglecting friction)

$\frac{p_a}{w} = \frac{p_b}{w} + \frac{v_b^2}{2g} - \frac{v_a^2}{w2g} - Z$

In practice the height $\inline Z$ is limited to avoid cavitation at $\inline A$ . (If there are no losses in the runner, the supply system or draft tube.)

Then the work done by the water on the runner (W.D.) $\inline = H - \displaystyle\frac{V_b^2}{2g}$ $\inline = H - \displaystyle\frac{V_1^2}{2g}$ (if there is no Draft tube or if it is parallel)

$\frac{V_wv - V_{w1}{v_1}}{gH}$

The Theoretical Hydraulic Efficiency $\inline \eta = \displaystyle\frac{Work\; Done}{H}$

Notes:

For a Reaction Turbine $\inline V\;\neq \sqrt{2gH}$
For Axial Flow $\inline v_1 = v$ . For radial flow $\inline \displaystyle\frac{v}{r} = \displaystyle\frac{v_1}{r_1} = \Omega = \displaystyle\frac{2\pi N}{60}$
Velocity of Flow

MISSING IMAGE!

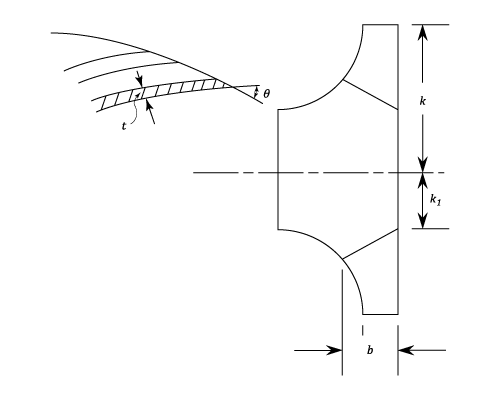
23287/Efficiency-of-Turbines-003.png cannot be found in /users/23287/Efficiency-of-Turbines-003.png. Please contact the submission author.

(NB. Reaction Turbines run full)

Let $\inline s$ be the number of blades, $\inline T$ the blade thickness and $\inline b$ the width of the

runner.

The circumferential area of flow at inlet is

$\left(2\pi r - s\,t\,cosec\theta \right)\;b\ = k\;2\pi r\,b$

where $\inline k$ is the blade factor

Therefore the rate of flow through the Turbine is

$Q = k\;2\pi r\;b\;V_f$

$\therefore\;\;\;\;\;V_f = \frac{Q}{k\,2\pi r\,b}$

Similarly at the outlet is

$\;V_{f1} = \displaystyle\frac{Q}{k_1\,2\pi r_1\,b_1}$

Unless otherwise stated it is normal to take $\inline k_1 = k$

Variations Of Pressure Head Across The Turbine Passage. Assuming No Losses

MISSING IMAGE!

23287/Efficiency-of-Turbines-tb.png cannot be found in /users/23287/Efficiency-of-Turbines-tb.png. Please contact the submission author.

Applying Bernoulli to the absolute flow

$\frac{p_x}{w} + \frac{V^2}{2g} = \frac{p_1}{w} + \frac{V_1^2}{2g} + \frac{V_wv - V_{w1}v_1}{g}$

or:

$\frac{p_1}{w} = \frac{p_x}{w} + \frac{V^2 - V_1^2}{2g} - \frac{V_wv - V_{w1}v_1}{g}$

Example:

[imperial]

Example - Example 1

Problem

In a Francis type Turbine, the guide-vane angle is 8 degrees, the inlet angle of the moving vanes is 110 degrees and the outlet angle is 20 degrees ( see diagram). Both the fixes and moving vanes reduce the flow by 15%.

The runner is 24 inches outside diameter and 16 inches inside diameter and the widths at the entrance and exit are 2 and 3 inches respectively.

The pressure at entry to the guides is + 87 ft.head and the kinetic energy there can be neglected. The pressure at discharge is - 6 ft.head.

If the losses in the guides and moving vanes are taken as $\displaystyle\frac{8\;f^2}{2g}$ where $f$ is the radial component of flow calculate:

a)The speed of the runner in r.p.m. for tangential flow on to the running vanes
b) The horse-power given to the runner by the water.

Workings

To find speed and horse-power.

Applying Bernoulli at the inlet to the guide vanes and the outlet of the runner.

$87 ft. = - 6ft + \frac{V_1^2}{2g} + \frac{V_wv + V_{w1}v_1}{g} + \frac{8V_f^2}{2g}$

From the velocity triangles ( above):

$V_w = V_f\;\tan\;82 = 7.115\;V_f$

$(v - V_w) = V_f\;tan\;20$

$\therefore\;\;\;\;\;v = V_f\;(\tan\;82 + \tan20) = 7.479\;V_f$

Also $V_{f1} = V_f$ . (Since $\pi Kdb = K_1\pi d_1b_1$ )

$v_1 = \frac{16}{24}\;v = \frac{2}{3}v\;=\frac{2}{3}\times 7.479\;V_f = 4.986\;V_f$

$(v_1 - V_{w1}) = V_{f1}\;\tan\,70 = 2.748\;V_f\;\;\;\;\;\;\;(V_f = V_{f1})$

$V_1 = \sqrt{V_{f1}^2 + V_{w1}^2} = 2.481\;V_f$

$\therefore\;\;\;\;93 = \left(\frac{(2.451)^2 + 2(7.115\times 7.479 - 2.238\times 4.986) + 8}{2g} \right)V_f^2$

Hence:

$V_f = 7.81\;ft/sec$

$\therefore\;\;\;\;\;v = 7.479\;V_f = 58.4\;ft/sec.$

But:

$v = \frac{\pi \,d\,N}{60}$

$\therefore\;\;\;\;\;N = \frac{60\times 58.4}{\pi \times 2} = 558\; r.p.m.$

Weight of water per second $W = K\;\pi \;d\;b\;w$

$= 0.85\times \pi \times 2\times \frac{1}{6}\times 7.81\times 62.4$

$= 434\;lb/sec$

Work Done per Lb. of water is given by:

W.D.

$= \frac{V_w\,v - V_{w1}\,v_1}{g} = \left(\frac{7.115V_f\times 7.479V_f - 2.238V_f\times 4.986V_f }{g}\right)$

$= \frac{42.06\times 7.81^2}{32.2} = 7.97 ft./lb/sec$

Horse-power

$= \frac{79.7\times 434}{550} = 62.9 H.P.\;\;( = 46.92 Kilo\;watts)$

Solution

a)The speed of the runner is $N= 558\; r.p.m.$
b) The horse-power given to the runner by the water is $46.92$ Kilo watts

Specific Speed Of A Turbine

Specific Speed This is the speed (r.p.m.) at which a similar model of the Turbine would run under a head of 1ft. when of such a size as to develop 1 Horse Power. The suffix "s" is used to denote the values associated with the Specific Turbine.

Each type of Turbine ( Pelton Wheel, Francis etc.) has it's own characteristic limits of $\inline N_s$ .

A similar model means :

Geometrically similar - made from the same drawings but to a different scale.
Dynamically similar - Operating conditions and equal efficiencies.

Thus in comparing two similar turbines all the linear dimensions will be in the same ratio. All angles will be the same; the velocity triangles will be geometrically similar and all velocities will be in the same ratio.

$V = K\sqrt{2gH}$

(3)

Therefore $\inline v\propto V_f\propto V\propto \sqrt{H}$

And

$v = \frac{\pi D\,N}{60}$

Therefore

$D \propto \frac{\sqrt{H}}{D}$

But $\inline Q$ = The Area of flow $\inline X$ the Velocity of flow

$\inline Q = K\,\pi \;D\;b\;V_f$ (and $\inline b\;\propto D$ ) or $\inline Q\;\propto \;D^2\;\sqrt{H}$

But the weight of water per second, $\inline W = w\;Q\;\propto \displaystyle\frac{H^{\frac{3}{2}}}{N^2}$

Thus the H.P.output of the Turbine is

$P = \displaystyle\frac{W\;H}{550}\times \eta \;\;\;\;\propto \;\;\;\displaystyle\frac{H^{\frac{5}{2}}}{N^2}$

(The efficiencies are equal)

$\therefore\;\;\;\;\;\frac{N\;\sqrt{P}}{H^{\frac{5}{4}}} = C = \frac{N_s\,\sqrt{P_s}}{H_s^{\frac{5}{4}}}$

(where $\inline C$ represents a Constant)

But for the specific Turbine $\inline P_s$ and $\inline H_s$ are 1.

$\therefore\;\;\;\;\;N_s = \frac{N\;\sqrt{P}}{H^{\frac{5}{4}}}$

MISSING IMAGE!

23287/SpecSpeed-and-Unit-Conditions-0006.png cannot be found in /users/23287/SpecSpeed-and-Unit-Conditions-0006.png. Please contact the submission author.

Notes On Specific Speed

$\inline N_s$ is based on the values of $\inline N$ , $\inline P$ , and $\inline H$ used at the design point. i.e. At maximum efficiency.
$\inline N_s$ is NOT dimensionless and there are different values in each of the measurement systems.

Unless otherwise stated, $\inline N$ is in r.p.m.
$\inline P$ is in Brake Horse Power(b.h.p.) ( $\inline \displaystyle\frac{ft\;lb/sec}{550}$ )
The unit of $\inline N_s$ are $\inline \displaystyle\frac{1}{T}\left(\displaystyle\frac{LM}{T^2}\displaystyle\frac{L}{T} \right)}^{\frac{1}{2}}\div L^{\frac{5}{4}}\= \displaystyle\frac{M^\frac{1}{2}}{T^\frac{5}{2}\;L^\frac{1}{4}}$
$\inline N_s$ can be made dimensionless and still be a constant by dividing by $\inline w^\frac{1}{2}\;g^\frac{3}{4}$ and this is called the Speed Number

For a particular type of Turbine $\inline N_s$ is constant.

$v = \displaystyle\frac{\pi \,D\,N}{60}$ and $v\propto \sqrt{H}$

Therefore $\inline N\propto \sqrt{H}$ or $\inline \displaystyle\frac{N}{\sqrt{H}}$ (constant)

but $\inline P = \displaystyle\frac{W\;H}{550}\times$ Efficience $\inline \propto W\;H\;\;\propto \;w\;Q\;H\;\propto D^2\V_f\H\;\propto H^\frac{3}{2}$

Therefore

$\displaystyle\frac{P}{H^\frac{3}{2}} = Constant$

and

$\sqrt{\frac{P}{H^\frac{3}{2}}}\times \frac{N}{\sqrt{H}} = \frac{N\sqrt{P}}{H^\frac{5}{4}}= N_s= Constant$

$\inline N_s$ for different types of Turbine and a comparison of heads for a particular power and speed.

The head requirements for a turbine to develop 100 b.h.p. at 1000r.p.m.

For a Pelton Wheel $\inline N_s\approx 4$ Head required 520 ft.
For a Turgot Turbine $\inline N_s\approx 7;to;15$ Head required 335 to 180ft
For a Francis Turbine $\inline N_s\approx15;to;100$ Head required 180 to 40ft
For a Propeller Turbine $\inline N_s\approx100;to;200^+$ Head required 40 to 23ft

An example of the use of Specific Speed $\inline N_s$

What turbine would be used if there was a supply of 10 cu.ft/sec under a head of 225 ft. ? Assume an efficiency of 80%.

Power Output = Water h.p.input $\inline X$ Efficiency

$= \frac{0.8\;w\;Q\,H}{550}\= \frac{0.8\times 62.4\times 10\times 225}{550} = 204\;h.p.$

$N_s = \frac{N\sqrt{P}}{H^\frac{5}{4}} = \frac{600\sqrt{204}}{225^\frac{5}{4}} = 9.83$

It would therefore be necessary to use a Turgot Turbine. However it might be possible to use a Pelton Wheel with two jets.

Power per jet $\inline = \displaystyle\frac{204}{2}$ h.p. Therefore $\inline N_s$ per Jet $\inline = \displaystyle\frac{9.83}{\sqrt{2}} = 6.95$

Try a Pelton Wheel with four Jets: $\inline N_s$ per Jet $\inline = \displaystyle\frac{9.83}{\sqrt{4}} = 4.92$

This would be a practical proposition but would result in some loss of efficiency due to interference between the jets. A better alternative would be to have two wheels on the same shaft with two jets per wheel.

Unit Conditions

Unit operating conditions for a turbine are those under which that particular turbine would run when working under a head of one ft. ( or unit head in any other system) assuming there to be change in efficiency.

To compare the performance of a given turbine when working under different heads and enables the characteristic curves to be drawn which show the efficiency at all running conditions:

Unit Speed $\inline N_u$

If $\inline N$ is the speed under a head $\inline H$

$v = \displaystyle\frac{\pi DN}{60}$

and $\inline v\propto V\propto H$ . Therefore, $\inline N\propto \sqrt{H}$

$\frac{N}{\sqrt{H}}= Constant =\frac{N_u}{\sqrt{H_u}}$

where $\inline u$ represents unit conditions.

Therefore the Unit speed is

$N_u=\frac{N}{\sqrt{H}}$

(4)

Unit quantity of a Turbine is the flow through the turbine when operating under a head of one ft. assuming similar conditions.

If $\inline Q =$ the flow under a head $\inline H$

$\inline Q =$ area of flow $\inline X$ velocity

And since the area is constant and the velocity is $\inline \propto \;\sqrt{H}$

$\inline Q\propto \sqrt{H}$ or $\inline \displaystyle\frac{Q}{\sqrt{H}}=$ Constant. Therefore, $\inline \displaystyle\frac{Q}{\sqrt{H}} = \displaystyle\frac{Q_u}{\sqrt{H_u}}$

Unit Power of a given turbine is the power output of the turbine when operating under a head of one ft. assuming no change in efficiency

If $\inline P$ is the output under a head $\inline H$ ,

Then $\inline P = \displaystyle\frac{W\;H}{550}\times \eta$

If $\inline \eta$ is unchanged $\inline W = wQ$

$\inline W\propto \sqrt{H}$ and $\inline P\propto \sqrt{H}\times H\;\;\;\;\propto H^\frac{3}{2}$

Therefore, $\inline \displaystyle\frac{P}{H^\frac{3}{2}} =$ Constant $\inline = \displaystyle\frac{P_u}{H_u^\frac{3}{2}}$

But, $\inline H_u = 1$ . Therefore, Unit Power, $\inline P_u = \displaystyle\frac{P}{H^\frac{3}{2}}$

MISSING IMAGE!

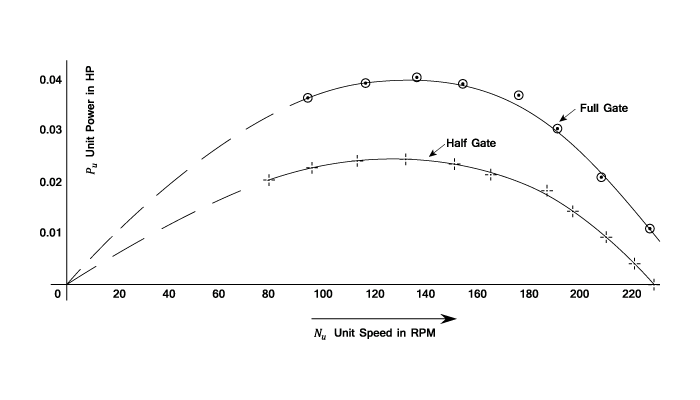
23287/SpecSpeed-and-Unit-Conditions-0021.png cannot be found in /users/23287/SpecSpeed-and-Unit-Conditions-0021.png. Please contact the submission author.

Note:

$N_u\sqrt{P_U} = \frac{N}{\sqrt{H}}\times \frac{\sqrt{P}}{H^\frac{3}{2}} = \frac{N\sqrt{P}}{H^\frac{5}{4}} = N_s$

Performance Curves Of A Turbine.

These are plotted for a constant head and a constant Gate opening ( Or needle valve setting) and are on the basis of speed in r.p.m.

MISSING IMAGE!

23287/SpecSpeed-and-Unit-Conditions-0016.png cannot be found in /users/23287/SpecSpeed-and-Unit-Conditions-0016.png. Please contact the submission author.

MISSING IMAGE!

23287/SpecSpeed-and-Unit-Conditions-0012-1.png cannot be found in /users/23287/SpecSpeed-and-Unit-Conditions-0012-1.png. Please contact the submission author.

MISSING IMAGE!

23287/SpecSpeed-and-Unit-Conditions-0012.png cannot be found in /users/23287/SpecSpeed-and-Unit-Conditions-0012.png. Please contact the submission author.

Characteristic Curves And Iso-efficiency Curves For A Turbine Under All Operating Conditions

The Turbine is tested under a constant head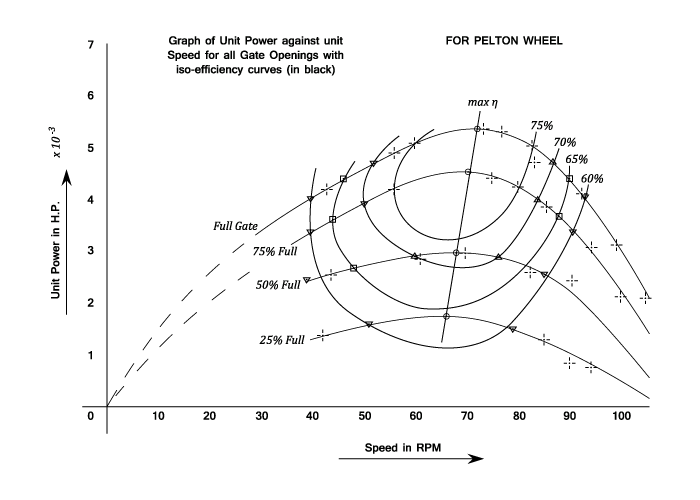 $\inline H$ for each of several gate openings and the values of Power output $\inline P$ and speed $\inline N$ are reduced to unit conditions ( Equations (125) (132)). Suitable values for efficiency are the marked on the curve for the differing Gate openings and lines of isoefficiency are drawn.

MISSING IMAGE!

23287/SpecSpeed-and-Unit-Conditions-0011.png cannot be found in /users/23287/SpecSpeed-and-Unit-Conditions-0011.png. Please contact the submission author.

These graphs enable the best running speed or the best gate opening to be chosen and the corresponding power output for that speed and gate setting to be found for any particular head.

Example of the use of unit conditions.

A Francis Turbine develops 3240 h.p. at 120 rpm when under a head of 36 ft. What would be the speed and output under a head of 25 ft. assuming no loss in efficiency.

$\inline N_u = \displaystyle\frac{N}{\sqrt{H}} = \displaystyle\frac{N_1}{\sqrt{H_1}}$ . Therefore, $\inline \displaystyle\frac{120}{\sqrt{36}} = \displaystyle\frac{N_1}{\sqrt{25}}$ . Therefore, $\inline N_1 = 100,r.p.m.$

But since $\inline H_u = 1$ , $\inline Q_u = \displaystyle\frac{Q}{\sqrt{H}}$

Unit Power, $\inline P_u = \displaystyle\frac{P}{H^\frac{3}{2}} = \displaystyle\frac{P_1}{H_1^\frac{3}{2}} = \displaystyle\frac{3240}{36^\frac{3}{2}} = \displaystyle\frac{P_1}{25^\frac{3}{2}}$

$\therefore\;\;\;\;\;P_1 = 1875\; h.p.$

The following theory assumes equal efficiencies for both the Model and the Prototype. For geometrically similar turbines operating under dynamically similar conditions, the velocity triangles will be similar and:

$v\propto V_f\propto V\propto \sqrt{H}$

But $\inline v = \displaystyle\frac{\pi DN}{60}$ . Therefore, $\inline \sqrt{H} = DN$ . Or $\inline \displaystyle\frac{\sqrt{H}}{DN} = C}$

And $\inline Q = K\pi DbV_f$ , $\inline b\propto D$ . Therefore $\inline Q\propto D^2\sqrt{H}$ . Or $\inline \displaystyle\frac{Q}{D^2\sqrt{H}} = C$ .

Substitute for $\inline H$ in the above equation: $\inline Q\propto ND^3$ . Or $\inline \displaystyle\frac{Q}{DN^3} =C$

Or substitute for $\inline D$ : $\inline Q\propto \displaystyle\frac{H}{N^2}\sqrt{H}$ Or $\inline \displaystyle\frac{QN^2}{H^\frac{3}{2}} = C$

Power, $\inline \displaystyle P = \frac{WH}{550} \times \eta$ if $\inline \eta$ is unchanged $\inline P\propto QH$ .

From Equation (146), $\inline P\propto D^2H^\frac{3}{2}$ . Or $\inline \displaystyle\frac{P}{D^2H^\frac{3}{2}} = C$

From Equation (148), $\inline P\propto \displaystyle\frac{H^\frac{3}{2}}{N^2}\times H$ . Or $\inline \displaystyle\frac{PN^2}{H^\frac{5}{2}} = C$

i.e. $\inline \displaystyle\frac{N\sqrt{P}}{H^\frac{5}{4}} = N_s = C$ (where $\inline C$ is a Constant)

From equations (144) and (150) $\inline P\propto D^2\propto D^3N^3$ . Or $\inline \displaystyle\frac{P}{N^3D^5} = C$

These seven expressions allow the performance of the prototype turbine to be estimated from tests on the model. Note that there are in fact only three independent equations.

The efficiency predicted for a large Turbine from test carried out on a model is usual lower than that obtained from the actual prototype. This is because of the relatively greater frictional losses in the smaller passages of the model.

Strictly speaking the surface finish of the model should be geometrically similar to that of the prototype. The reduction in efficiency is said to be due to scale effects and is corrected for in practice by the use of empirical equations such as:

The Moody equation

$\frac{1 - \eta _p}{1 - \eta _m} = \left(\frac{D_m}{D_p} \right)^\frac{1}{4}\left(\frac{H_m}{H_p} \right)^\frac{1}{10}$

Example:

[imperial]

Example - Example 1

Problem

A quarter scale Turbine is tested under a head of 36 ft.The full scale Turbine is required to work under a head of 100 ft.and to run at 428 r.p.m.

At what speed must the model be run and if it develops 135 h.p. and uses 38cu.ft.of water per second at this speed, what power will be obtained from the full scale Turbine, assuming that it's efficiency is 3% better than that of the model?

Workings

$\left(\frac{\sqrt{H}}{ND} \right)_m = \left(\frac{\sqrt{H}}{ND} \right)_p$

$\therefore\;\;\;\;\;\frac{N_m}{N_p} = \sqrt{\frac{H_m}{H_p}}\times \frac{D_p}{D_m} = \sqrt{\frac{36}{100}}\times 4 = \frac{24}{10}$

$\therefore\;\;\;\;\;N_m = 2.4\times 428 = 1027\;r.p.m.$

W.H.P. of the model $= \displaystyle\frac{62.4\times 38\times 36}{550} = 155\;h.p.$

$\therefore\;\;\;\;\;\eta _m = \left(\frac{P_m}{W.H.P.} \right) = \frac{135}{155} = 87.1\%$

$\therefore\;\;\;\;\;\eta _p = 90.1\%$

But

$\left(\frac{Q}{ND^3} \right)_m = \left(\frac{Q}{ND^3} \right)_p$

$\frac{(WHP)_p}{(WHP)_m} = \frac{Q_p\,H_p}{Q_m\,H_m} = \frac{N_pD_p^3}{N_mD_m^3}\times \frac{H_p}{H_m} = \frac{10}{24}\times 4^3\times \frac{100}{36}$

$= \frac{2000}{27}$

Therefore, WHP $= \displaystyle\frac{2000}{27}\times 155 = 11.500\;h.p.$

$P= 1150\times 0.901 = 10.360\;h.p.$

$N_s = \frac{N\sqrt{P}}{H^\frac{5}{4}} = \frac{428\sqrt{10.360}}{100^\frac{5}{4}} = 138$

With a value for $N_s$ of 138 the Turbine must be a Propeller Turbine.

Solution

The specific speed is $N_s=138$
The power is $10.360\;h.p.$