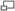Engineering › Fluid Mechanics › Fundamentals ›

Darcys formula

Darcy's formula for loss of head in pipe

View version details

Contents

Overview
Theory
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Henry Philibert Gaspard Darcy (1803-1858) was a French engineer who made several important contributions to hydraulics.

Overview

When the water is flowing in a pipe, it experiences some resistance to its motion, whose effect is to reduce the velocity and ultimately the head of water available. An empirical formula for the loss of head due to friction was derived by Henry Darcy.

The loss of head due to friction according to Darcy is,

$h_f = \frac{4flv^2}{2gd}$

where,

$\inline h_f$ = Loss of head due to friction
$\inline l$ = Length of pipe
$\inline d$ = Diameter of the pipe

Theory

Consider a uniform long pipe through which water is flowing at a uniform rate as shown in figure.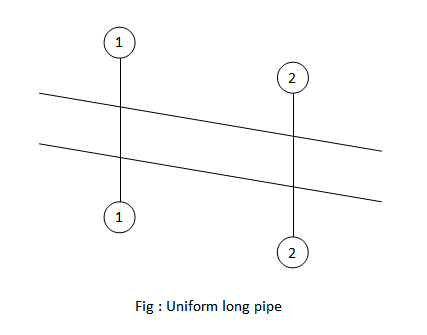

MISSING IMAGE!

23547/uniform_long_pipe.png cannot be found in /users/23547/uniform_long_pipe.png. Please contact the submission author.

Let,

$\inline v$ = Velocity of water in the pipe
$\inline f'$ = Frictional resistance per unit area at unit velocity

Consider sections (1-1) and (2-2) of the pipe Let,

$\inline p_1$ = Intensity of pressure at section (1-1)
$\inline p_2$ = Intensity of pressure at section (2-2)

A little consideration will show that p₁ and p₂ would have been equal, if there would have been no frictional resistance. Now considering horizontal forces on water between sections (1-1) and (2-2) and equating the same,

$p_1A = p_2A + Frictional\;Resistance$

$\Rightarrow Frictional\;Resistance = p_1A - p_2A$

Dividing both sides by $\inline w$ -

$\frac{Frictional\;Resistance}{w} = \frac{p_1A - p_2A}{w}$

$\Rightarrow \frac{Frictional\;Resistance}{Aw} = \frac{p_1}{w} - \frac{p_2}{w}$

But

$\frac{p_1}{w} - \frac{p_2}{w} = h_f = Loss\;of\;pressure\;due\;to\;friction$

$\therefore h_f = \frac{Frictional\;resistance}{Aw}$

$\Rightarrow h_f = \frac{Frictional\;resistance}{\frac{\pi}{4}\times d^2\times w}$

We know that as per Froude's experiment, frictional resistance

$h_f = Frictional\;resistance\;per\;unit\;area\;at\;unit\;velocity\times Wetted\;area\times (Velocity)^2$

$\Rightarrow h_f = f'\times \pi d l\times v^2$

Substituting the value of frictional resistance in the above equation,

$h_f = \frac{f'\pi dl\times v^2}{\frac{\pi}{4}\times d^2w} = \frac{4f'lv^2}{wd}$

Let us introduce another coefficient ( $\inline f$ ) such that,

$f' = \frac{fw}{2g}$

$\therefore h_f = \frac{4}{wd}\times \frac{fw}{2g}\times lv^2 = \frac{4flv^2}{2gd}$

(2)

We know that the discharge,

$Q = \frac{\pi}{4}\times d^2\times v$

$\Rightarrow v = \frac{4Q}{\pi d^2}$

$\therefore v^2 = \frac{16Q^2}{\pi^2 d^4}$

Substituting the value of $\inline v^2$ in equation (2)

$h_f = \frac{4fl}{2gd}\times \frac{16Q^2}{\pi^2 d^4} = \frac{flQ^2}{3d^5}$

(3)

Example:

[metric]

Example - Determination of the loss of head

Problem

Find the loss of head due to friction in a pipe of 500mm diameter and 1.5km long. The velocity of water in the pipe is 1.0 m/s. Take coefficient of friction as 0.005.

Workings

Given,

$d$ = 500 mm = 0.5 m
$l$ = 1.5 km = 1500 m
$v$ = 1 m/s
$f$ = 0.005

Since length of the pipe (1500 m) is more than 1000 d (1000*0.5 = 500m), therefore it is a long pipe. Now let us neglect all the minor losses except friction. We know that the loss of head due to friction,

$h_f = \frac{4flv^2}{2gd}$

$\Rightarrow h_f = \frac{4\times 0.005\times 1500\times (1)^2}{2\times 9.81\times 0.5}$

$\therefore h_f = 3.01\;m$

Solution

Loss of head due to friction = 3.01 m