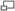CART

Tel: +44 (0) 20 7193 9303 Email Us Join CodeCogs

Engineering › Fluid Mechanics › Fundamentals ›

Eulers equation

Euler's equation for motion

Contents

Overview
Derivation Of Equation
Page Comments

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Overview

The Euler's equation for steady flow of an ideal fluid along a streamline is a relation between the velocity, pressure and density of a moving fluid. It is based on the Newton's Second Law of Motion. The integration of the equation gives Bernoulli's equation in the form of energy per unit weight of the following fluid.

It is based on the following assumptions:

The fluid is non-viscous (i,e., the frictional losses are zero).
The fluid is homogeneous and incompressible (i.e., mass density of the fluid is constant).
The flow is continuous, steady and along the streamline.
The velocity of the flow is uniform over the section.
No energy or force (except gravity and pressure forces) is involved in the flow.

Derivation Of Equation

Let us consider a steady flow of an ideal fluid along a streamline and small element AB of the flowing fluid as shown in figure.

25280/fig12.4.gif

Let,

dA = Cross-sectional area of the fluid element
ds = Length of the fluid element
dW = Weight of the fluid element
P = Pressure on the element at A
P+dP = Pressure on the element at B
v = velocity of the fluid element

We know that the external forces tending to accelerate the fluid element in the direction of the streamline

$= P.dA - (P+dP)dA$

$= -dP.dA$

We also know that the weight of the fluid element,

$dW = \rho g. dA.ds$

From the geometry of the figure, we find that the component of the weight of the fluid element in the direction of flow,

$= \rho g. dA.ds\cos \theta$

$= \rho g. dA.ds \frac{dz}{ds}$

$= \rho g. dA.dz$

$\inline \therefore$ Mass of the fluid element = $\inline \rho .dA.ds$

We see that the acceleration of the fluid element

$\frac{dv}{dt} = \frac{dv}{ds} \times \frac{ds}{dt} = v \frac{dv}{ds}$

Now, as per Newton's second law of motion, we know that Force = Mass *Acceleration

$\Rightarrow (-dp.dA)-(\rho g.dA.dz) = \rho.dA.ds\times v.\frac{dv}{ds}$

Dividing both sides by $\inline (-\rho dA)$

$\Rightarrow \frac{dP}{\rho}+g.dz = -v.dv$

or,

$\Rightarrow \frac{dP}{\rho}+g.dz+v.dv=0$

This is the required Euler's equation for motion as in the form of a differential equation. Integrating the above equation,

$\frac{1}{\rho}\int dP + \int g.dz + v.dv = Constant$

$\Rightarrow\frac{P}{\rho} + gz + \frac{v^2}{2} = Constant$

$\Rightarrow P + wz + \frac{wv^2}{2g} = Constant$

$\Rightarrow\frac{P}{w} + Z + \frac{v^2}{2g} = Constant$

or in other words,

$\frac{P_{1}}{w_{1}} + Z_{1} + \frac{v_{1}^2}{2g} = \frac{P_{2}}{w_{2}} + Z_{2} + \frac{v_{2}^2}{2g}$

which proves the Bernoulli's equation.