Engineering › Fluid Mechanics › Orifice › Flow From Tanks ›

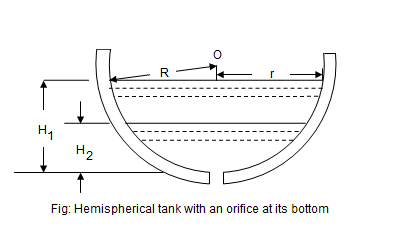
Hemispherical

Time of emptying a hemispherical tank through an orifice at its bottom

View version details

Contents

Overview
Page Comments

Overview

Consider a hemispherical tank, containing some liquid and having an orifice at its bottom as shown in figure.

Let,

$R$ = Radius of the tank
$H_{1}$ = Initial height of the liquid
$H_{2}$ = Final height of the liquid
a = Area of the orifice

At some instant, let the height of the liquid be h above the orifice.

We know that the theoretical velocity of the liquid at this instant, $v = \sqrt {2gh}$

At this instant, let r be the radius of the liquid surface.

Then the surface area of the liquid, $A = \pi r^2$

After a small interval of time dt, let the liquid level fall down by the amount dh.

Therefore volume of the liquid that has passed in time dt,

$dq = A \times (-dh) = -A.dh = -\pi r^2.dh$

(1)

The value of dh is taken as negative, as its value will decrease with the increase in discharge.

We know that the volume of liquid that has passed through the orifice in time dt,

$dq$ = Coefficient of discharge $\times$ Area $\times$ Theoretical velocity $\times$ Time

$\therefore dq = C_{d}.a.\sqrt {2gh}.dt$

(2)

Equating equations (1) and (2)

$-\pi r^2.dh = C_{d}.a.\sqrt {2gh}.dt$

(3)

From the geometry of the tank, we find that,

$r^2 = R^2 - (R - h)^2 = R^2 - R^2 + 2Rh - h^2 = 2Rh - h^2$

Substituting this value of $r^2$ in equation (3)

$-\pi (2Rh - h^2)dh = C_{d}.a.\sqrt {2gh}.dt$

$\therefore dt = \frac{-\pi (2Rh-h^2)dh}{C_{d}.a.\sqrt {2gh}} = \frac{-\pi (2Rh-h^2)\times h^{-\frac{1}{2}}.dh}{C_{d}.a.\sqrt {2g}}$

(4)

Now the total time T required to bring the liquid level from $H_{1}$ to $H_{2}$ may be found out by integrating the equation (4) between the limits $H_{1}$ to $H_{2}$ i.e.,

$T = \int_{H_{1}}^{H_{2}}\frac{-\pi (2Rh-h^2)\times h^{-\frac{1}{2}}.dh}{C_{d}.a.\sqrt {2g}}$

$\;\;\;\;= \frac{-\pi}{C_{d}.a.\sqrt {2g}}\int_{H_{1}}^{H_{2}}(2Rh^\frac{1}{2}-h^\frac{3}{2}).dh$

$\;\;\;\;= \frac{-\pi}{C_{d}.a.\sqrt {2g}}[\frac{4}{3}R(H_{2}^{\frac{3}{2}}-H_{1}^{\frac{3}{2}})-\frac{2}{5}(H_{2}^{\frac{5}{2}}-H_{1}^{\frac{5}{2}})]$

$\therefore T = \frac{2\pi}{C_{d}.a.\sqrt {2g}}[\frac{2}{3}R(H_{1}^{\frac{3}{2}}-H_{2}^{\frac{3}{2}})-\frac{1}{5}(H_{1}^{\frac{5}{2}}-H_{2}^{\frac{5}{2}})]$

If the vessel is to be completely emptied, then putting $H_{2}=0$ in this equation,

$T = \frac{2\pi}{C_{d}.a.\sqrt {2g}}[\frac{2}{3}RH_{1}^{\frac{3}{2}}-\frac{1}{5}H_{1}^{\frac{5}{2}}]$

If the vessel was full at the time of the commencement and is to be completely emptied, then putting $H_{1}=R$ in the above equation,

$T = \frac{14\pi R^{\frac{5}{2}}}{15C_{d}a\sqrt {2g}}$

Example:

[metric]

Example - Time of emptying a hemispherical tank

Problem

A hemispherical tank of 2 meters radius contains water up to a depth 1meter. Find the time taken to discharge the tank completely through an orifice of 1000 mm² provided at the bottom. Take $C_{d}$ = 0.62.

Workings

Given,

$R$ = 2m
$H_{1}$ = 1m
$a$ = 1000 mm²
$C_{d}$ = 0.62

We know that the time taken to discharge the tank completely.

$T = \frac{14\pi R^{\frac{5}{2}}}{15C_{d}a\sqrt {2g}}$

$\;\;\;\;= \frac{2\pi}{0.62\times 0.001\sqrt {2\times 9.81}}[\frac{2}{3}\times 2\times (1)^{\frac{3}{2}}-\frac{1}{5}\times (1)^{\frac{5}{2}}]$

$\;\;\;\;=2593 s = 43 min 13 s$

Solution

Time taken to discharge the tank completely = 43 min 13 sec