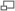Engineering › Fluid Mechanics › Orifice › Flow From Tanks ›

Square

Time of emptying a square, rectangular or circular tank through an orifice at its bottom

View version details

Overview

Consider a square, rectangular or circular tank of uniform cross-sectional area, containing some liquid and having an orifice at its bottom.

Let,

A = Surface area of the tank
$H_{1}$ = Initial height of the liquid
$H_{2}$ = Final height of the liquid
a = Area of the orifice

At some instant, let the height of the liquid be h above the orifice. We know that the theoretical velocity of the liquid at this instant, $v = \sqrt {2gh}$

After a small interval of time dt, let the liquid level fall down by the amount dh.

Therefore volume of the liquid that has passed in time dt,

$dq = A \times (-dh) = -A.dh$

(1)

The value of dh is taken as negative, as its value will decrease with the increase in discharge.

We know that the volume of liquid that has passed through the orifice in time dt,

$dq$ = Coefficient of discharge $\times$ Area $\times$ Theoretical velocity $\times$ Time

$\therefore dq = C_{d}.a.\sqrt {2gh}.dt$

(2)

Equating equations (1) and (2)

$-A.dh = C_{d}.a.\sqrt {2gh}.dt$

$\therefore dt = \frac{-A.dh}{C_{d}.a.\sqrt {2gh}} = \frac{-A.h^{-\frac{1}{2}}.dh}{C_{d}.a.\sqrt {2g}}$

(3)

Now the total time T required to bring the liquid level from $H_{1}$ to $H_{2}$ may be found out by integrating the equation (3) between the limits $H_{1}$ to $H_{2}$ i.e.,

$T = \int_{H_{1}}^{H_{2}} \frac{-A(h^{-\frac{1}{2}}).dh}{C_{d}.a.\sqrt {2g}}$

$\;\;\;\;= \frac{-A}{C_{d}.a.\sqrt {2g}}\int_{H_{1}}^{H_{2}}h^{-\frac{1}{2}}.dh$

$\;\;\;\;= \frac{-2A}{C_{d}.a.\sqrt {2g}}[\sqrt H_{2} - \sqrt H_{1}]$

Taking minus out from the bracket (as $H_{1}$ is greater than $H_{2}$ )

$T = \frac{2A(\sqrt H_{1}-\sqrt H_{2})}{C_{d}.a.\sqrt {2g}}$

If the tank is to be completely emptied, then putting $H_{2}$ = 0 in this equation, we get

$T = \frac{2A\sqrt H_{1}}{C_{d}.a.\sqrt {2g}}$

Example:

[metric]

Example - Time of emptying circular tank through an orifice at its bottom

Problem

A circular water tank of 4m diameter contains 5m deep water. An orifice of 400mm diameter is provided at its bottom. Find the time taken for water level fall from 5m to 2m. Take $C_{d}$ = 0.6

Workings

Given,

Diameter of circular tank, $D$ = 4m
Diameter of orifice, $d$ = 400mm = 0.4m
$H_{1}$ = 5m
$H_{2}$ = 2m
$C_{d}$ = 0.6

$\therefore$ The surface area of the circular tank,

$A = \frac{\pi}{4}\times D^2 = \frac{\pi}{4}\times 4^2 = 12.57m^2$

and the area of orifice,

$a = \frac{\pi}{4}\times d^2 = \frac{\pi}{4}\times 0.4^2 = 0.1257m^2$

$\therefore$ Time taken to fall the water level,

$T = \frac{2A(\sqrt H_{1}-\sqrt H_{2})}{C_{d}.a.\sqrt {2g}} = \frac{2\times 12.57\times (\sqrt 5-\sqrt 2)}{0.6\times 0.1257\times \sqrt {2 \times 9.81}} = 61.9s$

Solution

Time taken to fall the water level = 61.9 s