Engineering › Fluid Mechanics › Pipes › Mouthpiece ›

Convergent Mouthpiece

Discharge and Pressure in a Convergent Mouthpiece

View version details

Contents

Discharge Through A Convergent Mouthpiece
Pressure In A Convergent Mouthpiece
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Discharge Through A Convergent Mouthpiece

Generally a jet of liquid gets contracted at the entrance of a mouthpiece. There is always some loss of head due to this contraction of the jet. To counteract the loss of head, due to contraction of the jet up to vena contract, the mouthpiece is given the same slope as that of the jet of liquid as shown in fig-1.

MISSING IMAGE!

23547/convergent_1.png cannot be found in /users/23547/convergent_1.png. Please contact the submission author.

In such a mouthpiece, there will be no loss of head due to expansions. If such a mouthpiece terminates at the vena contracta of the jet, then the mouthpiece is called convergent mouthpiece.

Let,

$\inline H$ = Height of the liquid above the mouthpiece
$\inline a$ = Area of the orifice at point B, and
$\inline v$ = Velocity of the jet

Applying Bernoulli's equation to points A and B,

$H = \frac{v^2}{2g}$

$\Rightarrow v = \sqrt {2gH}$

$\therefore Actual\;Discharge,\;Q = Area\;of\;the\;orifice $\times$ Actual\;velocity$

$\Rightarrow Q = a\sqrt{2gH}$

(2)

We know that the actual discharge,

$Q = Coefficient\;of\;discharge $\times$ Area\;of\;orifice $\times$ Theoretical\;velocity$

$\Rightarrow Q = C_d.a\sqrt {2gH}$

(3)

Equating equation (2) and (3)

$a\sqrt {2gH} = C_d.a\sqrt {2gH}$

$\inline \therefore$ Coefficient of discharge, $\inline C_d$ = 1

and discharge, $\inline Q = a\sqrt {2gH}$

Example:

[metric]

Example - Discharge through a Convergent Mouthpiece

Problem

A convergent mouthpiece is discharging water under a constant head of 5m. Find the discharge, if diameter of the mouthpiece is 75 mm.

Workings

Given,

$H$ = 5m
$d$ = 75mm = 0.075m

The area of the mouthpiece,

$a = \frac{\pi}{4} \times (d)^2 = \frac{\pi}{4} \times (0.075)^2 = 4.418\times 10^{-3}\;m^2$

and discharge through the mouthpiece,

$Q = 1\times a\sqrt {2gH}$

$\Rightarrow 1\times (4.418\times 10^{-3})\times \sqrt {2\times 9.81\times 5} m^3/s$

$\Rightarrow Q = 0.0438\;m^3/s = 43.8\;liters/s$

Solution

Discharge through the mouthpiece = 43.8 liters/s

Pressure In A Convergent Mouthpiece

Consider a vessel, open to atmosphere at its top, having an orifice fitted with a convergent mouthpiece as shown in fig-2. We know that the slope of the mouthpiece is the same as that of the jet up to vena contracta.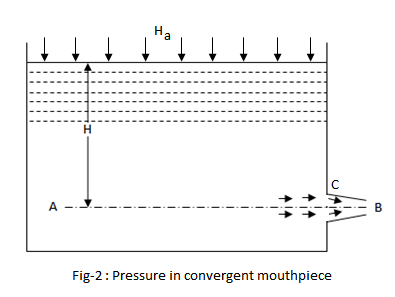

MISSING IMAGE!

23547/pressure_in_convergent.png cannot be found in /users/23547/pressure_in_convergent.png. Please contact the submission author.

Let,

$\inline H_a$ = Atmospheric pressure head
$\inline H$ = Height of liquid above the the mouthpiece
$\inline H_c$ = Absolute pressure head at vena contracta, and
$\inline v$ = Velocity of the jet

Applying Bernoulli's Equation to points A and C,

$H_a + H = H_c + \frac{v^2}{2g}$

$\Rightarrow H_c = H_a + H - \frac{v^2}{2g}$

(4)

If there is no loss of head, then

$H = \frac{v^2}{2g}$

Now substituting this value of H in equation (4)

$H_c = H_a + H - H = H_a$

This shows that the absolute pressure head at the vena contracta is the same as that of the atmosphere. But in actual practice, the flow is no longer a steady one.