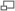Engineering › Fluid Mechanics › Pipes › Mouthpiece ›

Convergent_Divergent Mouthpiece

Discharge and Pressure in a Convergent - Divergent Mouthpiece

Contents

Overview
Discharge Through A Convergent-divergent Mouthpiece
Pressure In A Convergent-divergent Mouthpiece
Page Comments

Overview

In this type of mouthpiece, the mouthpiece is first made convergent up to the vena contracta of the jet and beyond that it is made divergent. Such a mouthpiece, which is first convergent is known as convergent-divergent mouthpiece as shown in figure.

Discharge Through A Convergent-divergent Mouthpiece

The discharge through a convergent-divergent mouthpiece is same as convergent mouthpiece. In such a mouthpiece, there will be no loss of head due to sudden expansion. The coefficient of discharge C_d in the case of convergent-divergent mouthpiece is also 1.

The diameter of the mouthpiece, for the purpose of calculating the discharge, is taken at the vena-contracta i.e., at C (or in other words where the convergent and divergent pieces meet). It is also known as throat diameter of the mouthpiece.

Example:

[metric]

Example - Discharge through a Convergent - Divergent Mouthpiece

Problem

A convergent-divergent mouthpiece having 80mm throat diameter is discharging water under a constant head of 4.5m. Find the discharge through the mouthpiece.

Workings

Given,

$\inline H$ = 4.5m
$\inline d$ = 80mm = 0.08m

The area of the mouthpiece,

$a = \frac{\pi}{4} \times (d)^2 = \frac{\pi}{4} \times (0.08)^2 = 5.027\times 10^{-3}\;m^2$

and discharge through the mouthpiece,

$Q = 1\times a\sqrt {2gH}$

$\Rightarrow 1\times (5.027\times 10^{-3})\times \sqrt {2\times 9.81\times 4.5}\;m^3/s$

$\Rightarrow Q = 47.2\times 10^{-3}\;m^3/s = 47.2\;liters/s$

Solution

Discharge through the mouthpiece = 47.2 liters/s

Pressure In A Convergent-divergent Mouthpiece

Consider a vessel open to atmosphere at its top, having an orifice fitted with a convergent-divergent mouthpiece as shown in fig-2. We know that the slope of the mouthpiece is the same as that of the jet up to vena contracta, and beyond that is it made divergent. The theoretical absolute pressure head at vena contracta is the same as that of atmospheric pressure head.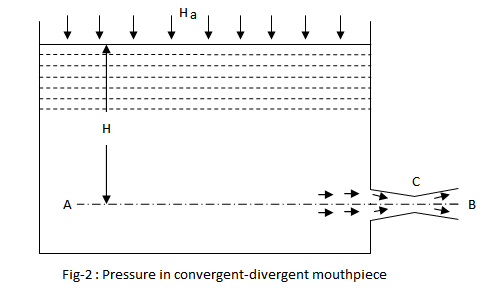

23547/pressurew_convergent-divergent.png

The pressure at the outlet of the mouthpiece is atmosphere. We know that the jet will expand from vena contracta (i.e., C) to outlet of the tube (i.e., B). For a steady flow, through the outlet of the mouthpiece, the shape of the divergent portion is made according to the profile of the expanding jet. However, if the divergence is made too large, the jet will not touch the walls of the mouthpiece.

Let,

$\inline H_a$ = Atmospheric pressure head
$\inline H$ = Height of liquid above the mouthpiece
$\inline H_c$ = Absolute pressure head at vena contracta
$\inline v$ = Velocity of liquid at outlet
$\inline v_c$ = Velocity of liquid at vena contracta
$\inline a_c$ = Area of mouthpiece at vena contracta
$\inline a$ = Area of mouthpiece at outlet

We know that, if there is no loss of head,

$H = \frac{v^2}{2g}$

$\Rightarrow v = \sqrt {2gH}$

Now applying Bernoulli's equation to points C and B,

$H_c + \frac{v_c^2}{2g} = H_a + \frac{v^2}{2g}$

(1)

Substituting the value of $\inline \frac{v^2}{2g}$ in (1)

$H_c + \frac{v_c^2}{2g} = H_a + H$

$\Rightarrow \frac{v_c^2}{2g} = H_a + H - H_c$

$\Rightarrow v_c = \sqrt {2g(H_a + H - H_c)}$

Since the flow of the liquid is continuous, therefore

$a_c.v_c = a.v$

$\Rightarrow \frac{a}{a_c} = \frac{v_c}{v} = \frac{\sqrt {2g(H_a + H - H_c)}}{\sqrt{2gh}} = \sqrt {1 + \frac{H_a + H_c}{H}}$

The above expression gives the ratio of areas of divergence to the convergence of the mouthpiece. If d and d_c be the diameters of the mouthpiece at outlet and vena contracta (i.e., convergence), then this expression can also be expressed as :

$\frac{\frac{\pi}{4}\times d^2}{\frac{\pi}{4}\times d_c^2} = \sqrt {1 + \frac{H_a - H_c}{H}}$

$\Rightarrow \frac{d^2}{d_c^2} = \sqrt {1 + \frac{H_a - H_c}{H}}$

Example:

[metric]

Example - Pressure in a Convergent - Divergent Mouthpiece

Problem

Water flows through a convergent-divergent mouthpiece of diameter at convergence 40mm, under a head of 4m. Determine the maximum diameter of divergence to avoid separation of the flow, if the maximum vacuum pressure is 8m of water.

Workings

Given,

$\inline d_c$ = 40mm = 0.04m
$\inline H$ = 4m
Maximum vacuum pressure head $\inline (H_a - H_c)$ = 8m

Let, $\inline d$ = Maximum diameter of the divergence in meters

We know that,

$\frac{d^2}{d_c^2} = \sqrt {1 + \frac{H_a - H_c}{H}}$

$\Rightarrow \frac{d^2}{0.04^2} = \sqrt {1 + \frac{8}{4}}$

$\Rightarrow d^2 = 1.732\times 0.004^2 = 2.77\times 10^{-3}$

$\Rightarrow d = 5.26\times 10^2\;m = 52.6\;mm$

Solution

Maximum diameter of the divergence, d = 52.6mm

Last Modified: 15 Jan 12 @ 08:46 Page Rendered: 2022-03-14 17:46:46