Engineering › Fluid Mechanics › Pipes › Mouthpiece ›

External Mouthpiece

Discharge and Pressure in an External Mouthpiece

View version details

Contents

Discharge Through An External Mouthpiece
Pressure In An External Mouthpiece
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Discharge Through An External Mouthpiece

The discharge through an orifice may be increased by fitting a sufficient length of pipe to the outside of the orifice as shown in figure. Such a pipe, which is attached externally to an orifice, is known as an external mouthpiece.

MISSING IMAGE!

23547/external_mouthpiece.png cannot be found in /users/23547/external_mouthpiece.png. Please contact the submission author.

A little consideration will show that the jet, on entering the pipe will first contract, then expand and fill up the whole pipe as shown in figure.

Let,

$\inline H$ = Height of liquid above the mouthpiece
$\inline a$ = Area of the orifice or mouthpiece
$\inline a_c$ = Area of flow at vena contracta
$\inline C_c$ = Coefficient of contraction
$\inline v$ = Velocity of liquid at outlet
$\inline v_c$ = Velocity of liquid at vena contracta

Assuming the coefficient of contraction at vena contracta to be 0.62, we have

$a_c = C_c\times a = 0.62 a$

Since the liquid is flowing continuously, therefore,

$v_c.a_c = v.a$

$\Rightarrow v_c = \frac{v.a}{a_c} = \frac{v}{0.62}$

We see that the jet after passing through the section 1-1, suddenly enlarges at section 2-2. Therefore due to the sudden enlargement the loss of head,

$\therefore h_c = \frac{(v_c-v)^2}{2g} = \frac{(\frac{v}{0.62}-v)^2}{2g} = \frac{0.375v^2}{2g}$

(2)

Applying Bernoulli's equation to point A and B,

$H = \frac{v^2}{2g} + Losses$

$\Rightarrow H = \frac{v^2}{2g} + \frac{0.375v^2}{2g}$

$\Rightarrow H = \frac{1.375v^2}{2g}$

$\therefore \frac{v^2}{2g} = \frac{H}{1.375}$

$\Rightarrow v = \frac{2gH}{1.375} = 0.855 \sqrt {2gH}$

(3)

We know that the theoretical velocity of liquid at the outlet = $\inline \sqrt {2gH}$

$\inline \therefore$ Coefficient of velocity,C_v = Actual velocity / Theoretical velocity

$\Rightarrow C_v = \frac{0.855\sqrt {2gH}}{\sqrt {2gH}} = 0.855$

(4)

Thus for finding the discharge, through an external mouthpiece, we shall first find out the value of coefficient of discharge for the mouthpiece. We know that coefficient of discharge (assuming $\inline C_c$ equal to 1)

$\inline C_d$ = Coefficient of velocity $\inline \times$ Coefficient of contraction = 0.855 $\inline \times$ 1 = 0.855

It shows that coefficient of discharge has considerably increased by fitting an external mouthpiece. The increase in coefficient of discharge means the increase in the discharge through the orifice.

$\inline \therefore$ Discharge, $\inline Q = C_d.a\sqrt {2gH} = 0.855.a\sqrt {2gH}$

It has been experimentally found that there is some loss of head at the entrance of the mouthpiece, depending upon the type of orifice. This loss of head, sometimes, reduces the coefficient of discharge by a small amount (up to 0.82). But, for all practical purposes, the value of coefficient of discharge is taken as 0.855.

The coefficient of discharge for an external mouthpiece also depends upon the length of the pipe. A little consideration will show that the coefficient of discharge will decrease, with the increase in length, due to greater frictional resistance offered by the walls of the mouthpiece to the flowing water.

If the length of the mouthpiece is not given, then the value of coefficient of discharge is taken as 0.855.

Example:

[metric]

Example - Discharge through an external mouthpiece

Problem

Find the discharge from a 100mm diameter external mouthpiece, fitted to one side of a large vessel, if the head over the mouthpiece is 4m.

Workings

Given,

$d$ = 100 mm = 0.1 m
$H$ = 4 m

We know that the area of the mouthpiece,

$a = \frac{\pi}{4}\times d^2 = \frac{\pi}{4}\times 0.1^2 = 0.0079m^2$

and discharge through an external mouthpiece,

$Q = 0.855.a.\sqrt {2gH} = 0.855 \times 0.0079 \times \sqrt {2\times 9.81\times 4}$

$= 0.0595 m^3/s = 59.5 liters/s$

Solution

$\therefore$ Discharge = 59.5 liters/s

Pressure In An External Mouthpiece

Consider a vessel, open to the atmosphere at its top, and having an orifice fitted with an external mouthpiece as shown in figure.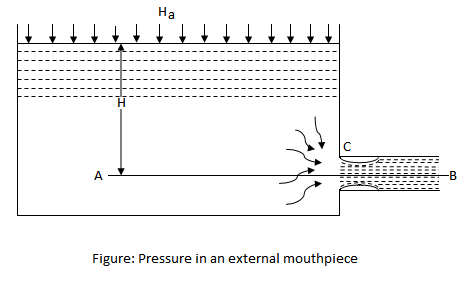

MISSING IMAGE!

23547/external_moputhpiece_2.png cannot be found in /users/23547/external_moputhpiece_2.png. Please contact the submission author.

We know that the jet of liquid on entering the mouthpiece, will first contract up to the vena contracta C and then expand and fill up the whole orifice as shown in figure.

Let,

$\inline H_a$ = Atmospheric pressure head
$\inline a$ = Height of liquid above the mouthpiece
$\inline H_c$ = Absolute pressure head at vena contracta
$\inline C_c$ = Coefficient of contraction
$\inline v$ = Velocity of liquid at outlet
$\inline v_c$ = Velocity of liquid at vena contracta

Applying Bernoulli's equation to point A and C

$H_a + H = H_c + \frac{{v_c}^2}{2g}$

$\Rightarrow H_c = H_a + H - \frac{v_c^2}{2g}$

Assuming coefficient of contraction to be equal to 0.62

$H_c = H_a + H - (\frac{v}{0.62})^2 \times \frac{1}{2g}$

$\Rightarrow H_c = H_a + H - (\frac{v^2}{2g} \times \frac{1}{0.62^2})$

(5)

From equation (3) we get

$\frac{v^2}{2g} = \frac{H}{1.375}$

Substituting the value of $\inline \frac{v^2}{2g}$ in equation (5)

$H_c = H_a + H - (\frac{H}{1.375} \times \frac{1}{0.62^2})$

$\Rightarrow H_c = H_a + H - 1.89H = H_a - 0.89H$

This shows that the absolute pressure head at vena contracta is less than the atmospheric pressure by an amount equal to 0.89 times the height of the liquid above the vena contracta. But, in actual practice, due to some loss of head at the entrance of the mouthpiece, the absolute pressure head at vena contracta reduces it by an amount equal to 0.74 times the height of the liquid at the vena contracta. But for all practical purposes, the absolute pressure at vena contracta is taken as,

$H_c = H_a - 0.89 H$

Example:

[metric]

Example - Pressure in an external mouthpiece

Problem

Water under a constant head of 5 meters is discharging through an external mouthpiece of 100 mm diameter. Determine the absolute pressure head of water at the vena contracta. Take atmospheric pressure as 10.3 m of water.

Workings

Given,

$H$ = 5m
$d$ = 100 mm = 0.1m
$H_a$ = 10.3 m

We know that the absolute pressure head of water at vena contracta of an external mouthpiece,

$H_c = H_a - 0.89 H$

$\Rightarrow H_c = 10.3 - (0.89 \times 5) = 5.88 m$

Solution

The absolute pressure head of water = 5.88 m