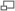Carnot Cycle
The ideal thermodynamic cycle
Overview
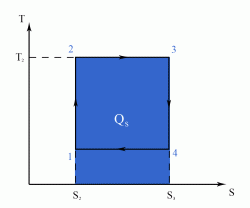
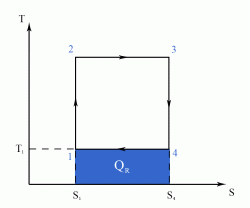
The Carnot Cycle is an entirely theoretical thermodynamic cycle utilising reversible processes. The thermal efficiency of the cycle (and in general of any reversible cycle) represents the highest possible thermal efficiency (this statement is also known as Carnot's theorem - for a more detailed discussion see also Second Law of Thermodynamics ). This ultimate thermal efficiency can then be used to compare the efficiencies of other cycles operating between the same two temperatures. The thermal efficiency of any engine working between the temperatures of T1 and T2 is: From equation (1) it can be seen that in order to improve the thermal efficiency of an engine, we should basically increase the value of (T2 - T1), i.e. increase the temperature difference under which the engine works.Thermal Efficiency
The thermal efficiency of a cycle, also denoted by
- a reversible adiabatic (i.e. isentropic) compression of the gas from temperature T1 to T2 (step 1-2),
- followed by an isothermal heating with expansion (step 2-3),
- then a reversible adiabatic (isentropic) expansion of the gas from T2 to T1 (step 3-4),
- and ending with an isothermal cooling with compression which reverts the system back to its initial state (step 4-1).
Example:
[imperial]
Example - Heat supplied to a steam engine
Problem
Consider a steam engine for which the steam is supplied at  and condensed at
and condensed at  . If the thermal efficiency of the steam engine is
. If the thermal efficiency of the steam engine is  of the Carnot efficiency, find the heat required (expressed in
of the Carnot efficiency, find the heat required (expressed in  ) to produce a work output of 1 horsepower (
) to produce a work output of 1 horsepower ( ) for 1 minute.
) for 1 minute.
Workings
We know that the Carnot efficiency of an engine working between temperatures  and
and  is given by:
where
is given by:
where  and
and  are absolute temperatures expressed in kelvins (
are absolute temperatures expressed in kelvins ( ).
Therefore, in order to calculate the Carnot efficiency of the steam engine from the hypothesis, we first have to convert the temperatures into absolute temperatures. As we have that:
and
we get the Carnot efficiency of the steam engine:
from which we obtain:
or, expressed as percentage:
As the actual efficiency of the steam engine is
).
Therefore, in order to calculate the Carnot efficiency of the steam engine from the hypothesis, we first have to convert the temperatures into absolute temperatures. As we have that:
and
we get the Carnot efficiency of the steam engine:
from which we obtain:
or, expressed as percentage:
As the actual efficiency of the steam engine is  of the Carnot efficiency, we can calculate the actual efficiency
of the Carnot efficiency, we can calculate the actual efficiency  as:
from which we obtain:
or, expressed as percentage:
We know that the thermal efficiency of an engine is given by:
where
as:
from which we obtain:
or, expressed as percentage:
We know that the thermal efficiency of an engine is given by:
where  is the work output, and
is the work output, and  the heat supplied. Therefore, the heat supplied
the heat supplied. Therefore, the heat supplied  in order to produce a work output of
in order to produce a work output of  , while working at an efficiency of
, while working at an efficiency of  can be written as:
From the hypothesis we have that the required work output
can be written as:
From the hypothesis we have that the required work output  is
is  for
for  . Taking into account that
. Taking into account that  , the work
, the work  can also be expressed in
can also be expressed in  as:
from which we obtain:
By using (13) and (8) in equation (11), and also considering that
as:
from which we obtain:
By using (13) and (8) in equation (11), and also considering that  , we get the heat required (expressed in
, we get the heat required (expressed in  ) to produce
) to produce  for
for  as:
from which we obtain:
as:
from which we obtain:
Solution
 Login
Login