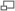Cantilever Beams
Formulae for the shear and deflection of Cantilever Beams under a selection of differing loadings.
Contents
- Overview
- Fixed At One End With A Uniform Load.
- Fixed At One End. Load At The Other
- Fixed At One End. Load Intermediate.
- Fixed At One End. Supported At The Other. Uniform Load.
- Fixed At One End, Supported At The Other With A Central Point Load.
- Fixed At One End And Free But Guided At The Other. Uniform Load.
- Fixed At One End. Free But Guided At The Other. Point Load.
- Page Comments
Overview
This section covers Beams used as Cantilever. The examples include Beams which are "Built-in" at one end and either supported or guided at the other.Fixed At One End With A Uniform Load.
The stress is given by: ^2) The Stress at the Support:
The Stress at the Support:  If the cross section is Constant then this is the maximum stress.
The Deflection is given by:
If the cross section is Constant then this is the maximum stress.
The Deflection is given by: ^2]) The Maximum deflection is at the end and is:
The Maximum deflection is at the end and is: 
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.
Fixed At One End. Load At The Other

The Stress is given by: ) The Stress at the Support:
The Stress at the Support:  If the Cross-Section is Constant, then this is the Maximum Stress.
The Deflection at any point is given by:
If the Cross-Section is Constant, then this is the Maximum Stress.
The Deflection at any point is given by: ) The Maximum Deflection is at the end and is:
The Maximum Deflection is at the end and is: 
Deflection is a term that is used to describe the degree to which a structural element is displaced under a load.
Fixed At One End. Load Intermediate.
Between the Fixed End and the Load: ) Beyond the Load the stress is zero.
At the Fixed End:
Beyond the Load the stress is zero.
At the Fixed End:  If the Cross-section is Constant, then this is the Maximum Stress.
The Deflection of any point between the Fixed end and the Load is:
If the Cross-section is Constant, then this is the Maximum Stress.
The Deflection of any point between the Fixed end and the Load is: ) Beyond the load the Deflection is:
Beyond the load the Deflection is: ) The Maximum Deflection at the "Free" end is:
The Maximum Deflection at the "Free" end is: ) Deflection at the Load:
Deflection at the Load: 
Fixed At One End. Supported At The Other. Uniform Load.

The Stress at any point is : }{2\;Z\;l}\;\;\left(\displaystyle\frac{1}{4}\;l&space;-&space;x&space;\right)) The Maximum Stress at the Fixed End:
The Maximum Stress at the Fixed End:  The Stesss is zero at
The Stesss is zero at  . The greatest negative Stres is at
. The greatest negative Stres is at  and is:
and is:
 The deflection is given by:
The deflection is given by: }{48\;E\;I\;l}\;\;(3\;l&space;-&space;2\;x)) The maximum Deflection is at x = 0.5785 l and is:
The maximum Deflection is at x = 0.5785 l and is:  The Deflection at the centre is:
The Deflection at the centre is:  The Deflection at the point of greatest negative Stress, i.e. at
The Deflection at the point of greatest negative Stress, i.e. at  , is:
, is:

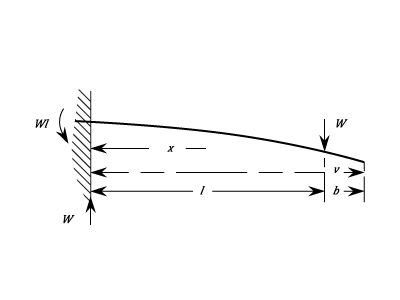
Fixed At One End, Supported At The Other With A Central Point Load.
The Stress between the Fixed Point and the Load: ) Between the Support and the Load:
Between the Support and the Load:  Stress at the Fixed end. This is the maximum value
Stress at the Fixed end. This is the maximum value  The Stress is Zero at
The Stress is Zero at  The Greatest negative Stress is at the centre and is
The Greatest negative Stress is at the centre and is  The Deflection of any Point between the Fixed End and the Load:
The Deflection of any Point between the Fixed End and the Load:
) The Deflection of any Point between the Support and the Load
The Deflection of any Point between the Support and the Load
) The Maximum Deflection is at
The Maximum Deflection is at 
 The Deflection of the Load is:
The Deflection of the Load is: 
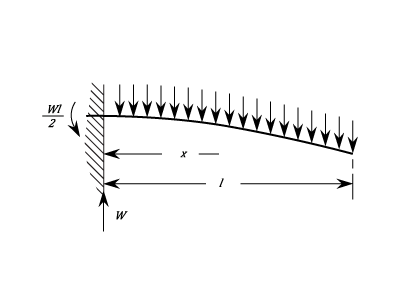
Fixed At One End And Free But Guided At The Other. Uniform Load.
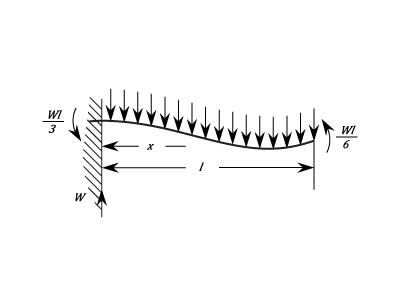
The Stress at any Point ^2&space;\right\}) The Maximum Stress is at the support and is
The Maximum Stress is at the support and is  The Stress is zero when
The Stress is zero when  The Greatest negative stress is at the free end and is
The Greatest negative stress is at the free end and is  The Deflection at any Point is given by:
The Deflection at any Point is given by: ^2) The Maximum Deflection is at the free end and is:
The Maximum Deflection is at the free end and is: 
Fixed At One End. Free But Guided At The Other. Point Load.
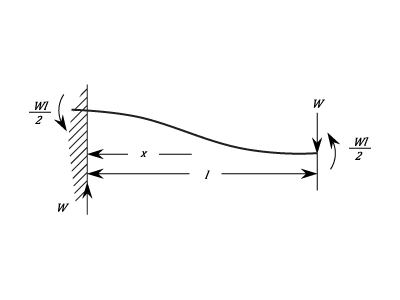
Stress at any Point: ) The Stress at the Support
The Stress at the Support  The Stress at the Free End:
The Stress at the Free End:  These are the Maximum Stresses and are equal and opposite. The Stress is zero at the Centre.
The Deflection at any Point is:
These are the Maximum Stresses and are equal and opposite. The Stress is zero at the Centre.
The Deflection at any Point is: ) The Maximum Deflection is at the Free End and is:
The Maximum Deflection is at the Free End and is: 
 Login
Login